The optical properties of crystals are intimately related to their crystal structures. This article examines the precise relationship between optic character and sign and crystal structure.
Optic character/sign with the jeweler's refractometer
The jeweler's refractometer is a powerful tool, but a fundamental understanding of the optical properties of crystals is needed to use it to its maximum potential.
Most gemologists are aware that, given a well-polished flat facet, the refractometer can determine the refractive index (RI) of a gem, and also the full birefringence of a doubly refractive gem. However many gemologists do not understand that the following can also be calculated on any single facet of a gem so long as the facet being tested gives clear readings:
- Optic character: Single refraction (SR), double refraction (DR), and further for DR gems, uniaxial (U) or biaxial (B) optic character.
- Optic sign: (+, –, or neutral).
In order to determine optic character and sign, a few tricks must be learned. This article is an attempt to teach the tricks that unlock the power of the jeweler's refractometer.
What is refractive index (RI)?
Refractive index is a measure of the optical density of a material. In a vacuum (and air is close enough to represent a vacuum), light travels at approximately 300,000 km/second. When it enters a more optically dense material, it slows down (and if the entry angle is oblique, it is also bent or 'refracted' towards the normal). Refractive index represents a ratio between the speed of light in a vacuum vs. the speed of light in another material. In other words, it explains how much light slows down in other more optically dense materials. Spinel has an RI of about 1.72. This means light travels 1.72 times slower in spinel than in a vacuum (or air).
Fraunhofer lines
If one points a spectroscope at the sky, a series of dark absorption lines will be seen. These were first discovered by the English chemist, William Hyde Wollaston in 1802, but as is often the case, the original discoverer doesn't get credit. The German scientist, Joseph von Fraunhofer, independently rediscovered them and are now named after Fraunhofer. These absorption lines are caused by the gases surrounding the Sun and Earth, and represent reference points in the visible spectrum.
What is dispersion?
Dispersion is defined as a variation of RI with wavelength. It so happens that RI is dependent on the wavelength of light used to measure it. Different wavelengths will be slowed (and refracted) by different amounts, and thus have different refractive indices. Thus if we are to measure RI in a material, we need to have a standard wavelength of light against which to measure it. The standard wavelength for measuring RI is using the Fraunhofer D line (589 nm), which is produced by sodium. All refractive measurements are thus noted as nD, meaning that the RI was measured using light of a wavelength of 589 nm.
Dispersion manifests itself in faceted gems as a splitting of white light into its spectral colors when it travels through non-parallel surfaces. We call this "fire."
In gemology, dispersion is measured by measuring the RI of a substance using light of the Fraunhofer B line (red; 687 nm) and then with the Fraunhofer G line (violet; 431 nm). The differences in RI is the dispersion of the substance, and is also known as the B-G interval. The B-G interval in diamond is 0.044.
Regarding the refractometer, what is important is to understand that in order for RI's to be compared with one another, they must be measured using light of the same wavelength. Yellow light corresponding to the Fraunhofer D line (589 nm) was chosen as the standard. Because yellow is the narrowest color in the solar spectrum, so long as your light source is yellow, your RI should be close to that measured with a pure sodium Fraunhofer D source.
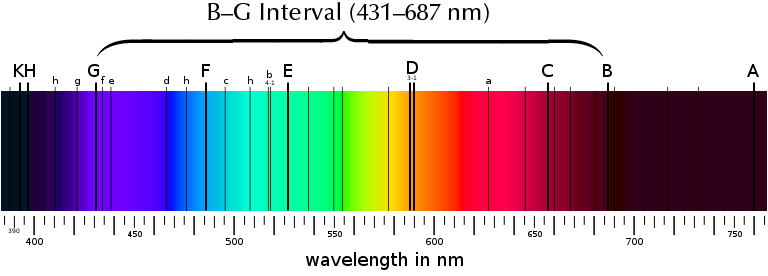 Figure 1. Fraunhofer lines in the solar spectrum. These are used as reference points. All refractive indices are calibrated for light of 589 nm, matching the Fraunhofer D line (nD). Dispersion in gemology is measured as the difference in RI between the Fraunhofer B and G lines.
Figure 1. Fraunhofer lines in the solar spectrum. These are used as reference points. All refractive indices are calibrated for light of 589 nm, matching the Fraunhofer D line (nD). Dispersion in gemology is measured as the difference in RI between the Fraunhofer B and G lines.
How does the refractometer work?
The jeweler's refractometer utilizes the concept of total internal reflection to reveal the RI of a gem placed into optical contact with the prism/hemicylinder. The refractometer displays the point at which total internal reflection occurs as a shadow edge against a calibrated scale. This is the point where the RI reading is taken.
- To create an optical contact, a contact liquid with an RI between the RI of the prism/hemicylinder and the gem being tested must be used. The highest RI of any liquid that is reasonably safe to use in a non-lab environment is 1.81. Thus this is the de facto limit to RI measurements using the jeweler's refractometer. Should non-toxic liquids of higher RI be developed, this would push the high RI limit past the current 1.81 limit.
RI curves vs. actual lab practice
In the material that follows, refractive indices will be plotted out graphically as the stone is rotated through 180° on the refractometer hemicylinder/prism. In actual practice, RI readings of DR gems should be taken as follows:
- Using the refractometer eyepiece polaroid plate, isolate the lower of the two curves. Then rotate the gem bit by bit, readjusting the polaroid plate to maintain isolation of the lower RI curve, while noting its minimum and maximum readings. These are then noted down.
- Repeat the process for the high RI curve
- The end result is something like this: Low curve = 1.762 to 1.770; High curve = 1.770 to 1.770
From these readings, we can see that the low RI curve goes from 1.762 to 1.770, while the high RI curve is constant at 1.770. Using the pattern matching described below, the result would be DR U–.
Overview of the crystal systems and their symmetry and optical properties
| Structure | Structure type Crystal axes Angles |
Symmetry (of highest crystal class) | Optic character | Refractive index (RI) |
Optic sign | Pleochroism | Gem examples |
| Amorphous | No order
No axes |
No symmetry | Isotropic
Singly refractive |
1 RI |
None | None | Glass
Amber |
| Cubic | Isometric: 1 axis length
a1 = a2 = a3 |
13 planes
9 axes |
Isotropic
Singly refractive |
1 RI
n |
None | None |
Diamond |
| Tetragonal | Dimetric: 2 axis lengths
a1 = a2 ≠ c |
5 planes
5 axes |
Anisotropic
Doubly refractive |
2 RIs nω and nε |
+ = nε > nω
– = nε < nω |
May be dichroic | Zircon |
| Hexagonal | Dimetric: 2 axis lengths
a1 = a2 = a3 ≠ c |
7 planes
7 axes |
Anisotropic
Doubly refractive |
2 RIs nω and nε
|
+ = nε > nω
– = nε < nω
|
May be dichroic | Beryl
Apatite |
| Trigonal | Dimetric: 2 axis lengths
a1 = a2 = a3 ≠ c |
3 planes
4 axes |
Anisotropic
Doubly refractive |
2 RIs
nω and nε |
+ = nε > nω
– = nε < nω
|
May be dichroic | Corundum
Quartz |
| Orthorhombic | Trimetric: 3 axis lengths
a ≠ b ≠ c |
3 planes
3 axes |
Anisotropic
Doubly refractive |
3 RIs
nα, nβ, nγ |
+ = nβ closer to nα
– = nβ closer to nγ ± = nβ midway to nα & nγ |
May be trichroic | Topaz
Zoisite |
| Monoclinic | Trimetric: 3 axis lengths
a ≠ b ≠ c |
1 axis
1 plane |
Anisotropic
Doubly refractive |
3 RIs
nα, nβ, nγ |
+ = nβ closer to nα
– = nβ closer to nγ |
May be trichroic | Orthoclase
Spodumene |
| Triclinic | Trimetric: 3 axis lengths
a ≠ b ≠ c |
No planes
No axes |
Anisotropic
Doubly refractive |
3 RIs
nα, nβ, nγ |
+ = nβ closer to nα
– = nβ closer to nγ |
May be trichroic | Axinite
Labradorite |
Optic character/curve variations: Uniaxial or biaxial?
- Two constant curves = Uniaxial
- Two variable curves = Biaxial
- One constant/one variable, which meet but do not cross = Uniaxial
- One constant/one variable which don't meet
- Check the polaroid angle of the constant curve
- Biaxial = polaroid angle of constant curve = 90°
- Uniaxial = polaroid angle of constant curve ≠ 90°
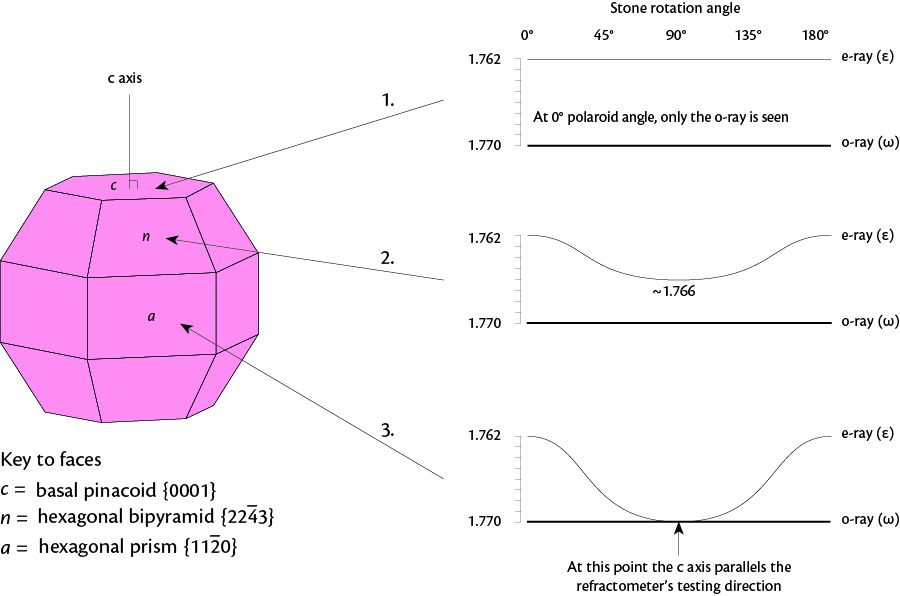 Figure 2. RI readings for different faces on corundum. Corundum is uniaxial negative. Illustration © Richard W. Hughes
Figure 2. RI readings for different faces on corundum. Corundum is uniaxial negative. Illustration © Richard W. Hughes
Symbols
Uniaxial crystals
- nω = omega, the constant RI of a uniaxial crystal which is found when light vibrates in the plane of the a axes
- nε = epsilon, the RI of a uniaxial crystal when light vibrates parallel to c. This is found only when light travels perpendicular to c.
Biaxial crystals
- nα = alpha, the lowest RI of a biaxial crystal = light vibrating parallel to the X optical direction
- nβ = beta, the intermediate RI of a biaxial crystal = light vibrating parallel to the Y optical direction, or along one of the two optic axes
- nγ = gamma, the highest RI of a biaxial crystal = light vibrating parallel to the Z optical direction
Optic sign
Uniaxial stones
- High RI curve varies = (+)
- Low RI curve varies = (–)
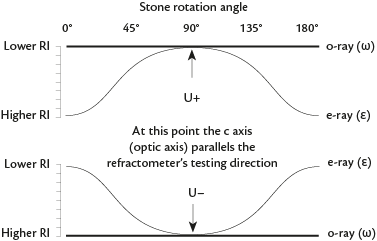
- Both curves constant: At 0° polaroid angle, only the o-ray is seen
- a. If low curve is seen = (+)
- b. If high curve is seen = (–)
Biaxial stones
- If nβ is closer to nα, the gem is (+)
- If nβ is closer to nγ, the gem is (–)
- If nβ is halfway between nα and nγ, the gem is (±)
Finding beta
- If two possible betas exist (neither curve crosses the midpoint), false beta will have a polaroid angle equal to 90°. True beta will have a polaroid angle unequal to 90°.
- In biaxial stones, beta is the highest RI of the low curve or the lowest RI of the high curve, where the curve passes a point midway between nα and nγ.
- In biaxial stones, beta is the point where the two curves meet or cross.
- In biaxial stones, if one reading is constant and the other varies, beta is the extreme intermediate point of the variable curve.
- If both curves vary and neither crosses the midpoint, false beta will have a polaroid angle equal to 90°. True beta will have a polaroid angle unequal to 90°.
Polaroid angle
- 0° polaroid angle is when the transmission direction of the polaroid plate is parallel to the refractometer scale divisions.
- 90° polaroid angle is when the transmission direction of the polaroid plate is perpendicular to the refractometer scale divisions.
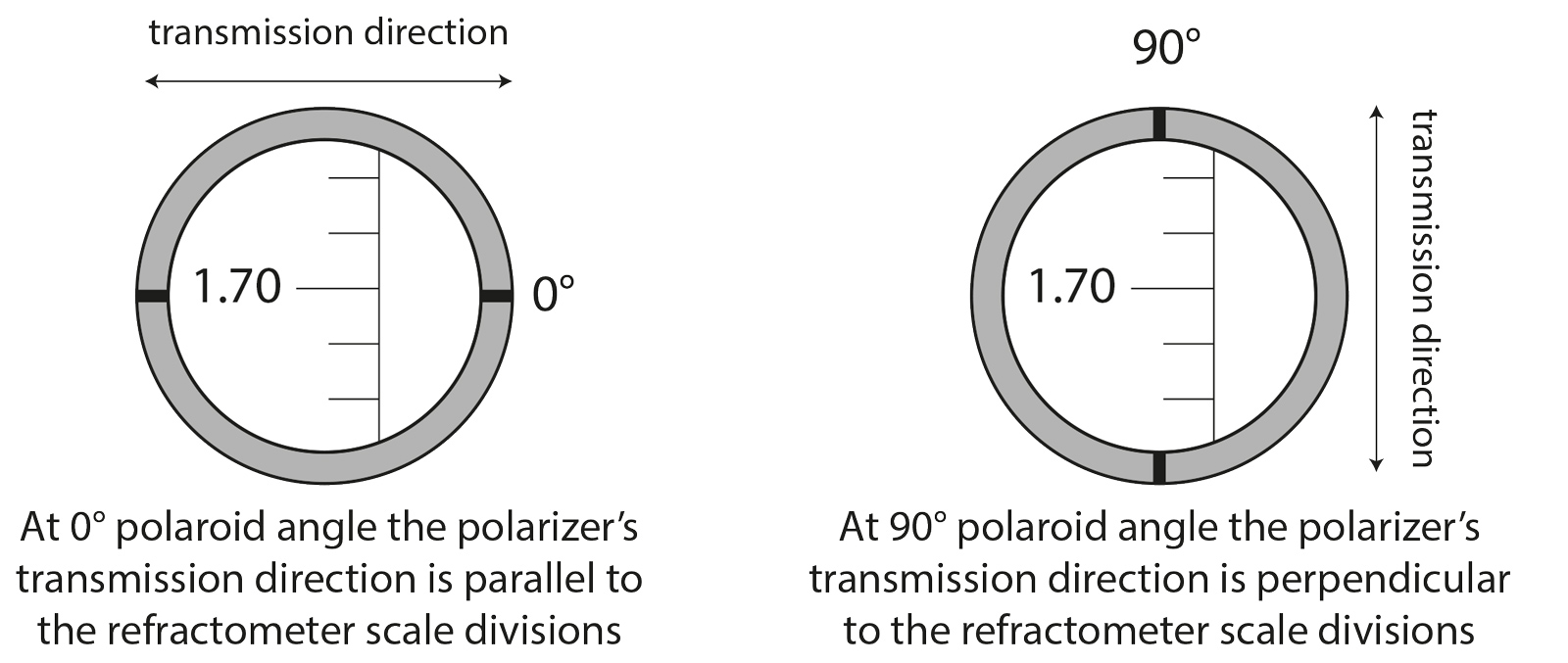 Figure 3. Use of the refractometer polaroid angle can help to determine both optic character and sign from any single facet on any stone. The 0° angle is when the transmission direction of the refractometer eyepiece polarizer is parallel to the scale divisions of the refractometer. One can easily determine the transmission direction of the eyepiece polarizer by rotating it in front of an LCD computer monitor and noting the direction of strongest light transmission. The edge of the filter than then be marked, as shown above. Illustration © Richard W. Hughes. Click on the figure for a larger example.
Figure 3. Use of the refractometer polaroid angle can help to determine both optic character and sign from any single facet on any stone. The 0° angle is when the transmission direction of the refractometer eyepiece polarizer is parallel to the scale divisions of the refractometer. One can easily determine the transmission direction of the eyepiece polarizer by rotating it in front of an LCD computer monitor and noting the direction of strongest light transmission. The edge of the filter than then be marked, as shown above. Illustration © Richard W. Hughes. Click on the figure for a larger example.
Overview of the crystal systems and their optical properties
| Optic Character Type | RI Pattern | Optic Sign Determination | Crystal Orientation | RI Curves |
|
Amorphous and Isometric |
Single RI in all directions | N/A | N/A |  |
| Dimetric = Uniaxial | Two constant RIs | At 0° polaroid angle, only o-ray is seen;
|
C axis perpendicular to facet tested |  |
| One constant and one variable curve that meet but do not cross |
|
C axis is parallel to the facet tested. When c is parallel to the refractometer testing direction the curves come together (only a single RI is visible) |
 |
|
| One constant and one variable curve that do not meet or cross |
|
C axis is oblique to the facet tested. Polaroid angle of the constant curve ≠ 90° |
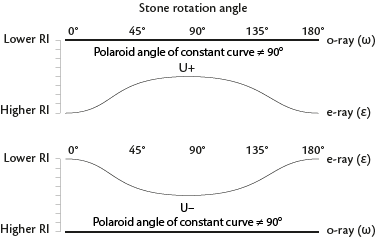 |
|
| Trimetric = Biaxial | Constant low RI |
|
X axis is perpendicular to the facet tested | 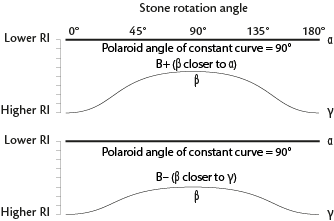 |
| Constant intermediate RI |
|
Y axis is perpendicular to the facet tested | 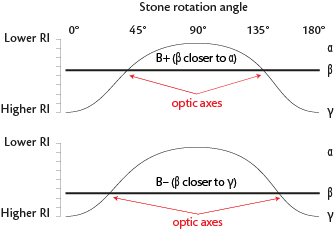 |
|
| Constant high RI |
|
Z axis is perpendicular to the facet tested | 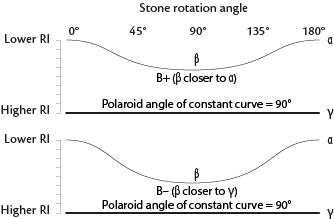 |
|
| One constant and one variable curve that do not meet or cross |
|
Z direction perpendicular to the facet tested | 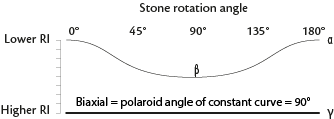 |
|
| Two variable curves, neither crossing the midpoint |
|
Random section | 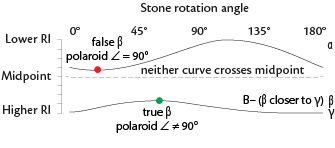 |
|
| Two variable curves, one crossing the midpoint |
|
Random section | 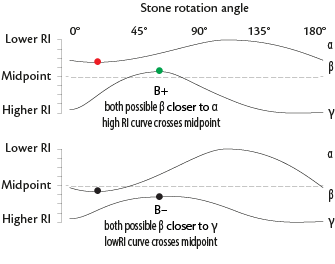 |
Author's Notes
The above technique for determining the optic character and sign with the jeweler's refractometer was first developed by Dr. Cornelius Hurlbut:
- Hurlbut, C.S. (1984) The jeweler's refractometer as a mineralogical tool. American Mineralogist, Vol. 69, pp. 391–398.
The technique is also detailed in the second edition (but not the first) of his book, Gemology.
-
Hurlbut, C.S. and Kammerling, R. (1991) Gemology. New York, NY, Wiley, 2nd ed., 337 pp.
The technique has also been beautifully described as well by:
- Sturman, Darko (2005) Use of the polarizing filter on the refractometer. Journal of Gemmology, Vol. 29, No. 5/6, pp. 341–348.
I have reversed the polaroid angles of Hurlbut as I find it easier to remember relative to the refractometer scale divisions.
For more on crystal optics, see:
-
Hughes, R.W. (2014) Pleochroism in faceted gems: An introduction. Gems & Gemology, Vol. 50, No. 3, Fall, pp. 216–226.